Fabulous Info About How To Tell If A Matrix Is Diagonalizable

True or false and explain why?: The diagonalizable matrices are those that have no defective eigenvalues (i.e., eigenvalues whose geometric multiplicity is less than their algebraic multiplicity). See the proofs of the theorems on eigenbasis,.

how to prepare for spring break how to stop a program on start up how to manage sales people how to reduce muscular legs how to reduce substance p how to reduce high blood sugar levels how to start a copy store how to repair uneven lawn

6. Diagonalizable Matrix Youtube

Show That A Matrix Is Diagonalizable Youtube

Garbage Can Berry How To Tell If A Jordan Block Is

Ppt Mac 2103 Powerpoint Presentation, Free Download Id584999

Ppt Diagonal Matrix Powerpoint Presentation, Free Download Id5424371

Linear Algebra Matrix Diagonalization Youtube

How to diagonalize a matrix?

How to tell if a matrix is diagonalizable. The first theorem about diagonalizable matrices shows that a large class of matrices is automatically diagonalizable. A matrix is diagonalizable if it is similar to a diagonal matrix. The 4 ways to tell if a matrix is diagonalizable [passing linear algebra] stem support.

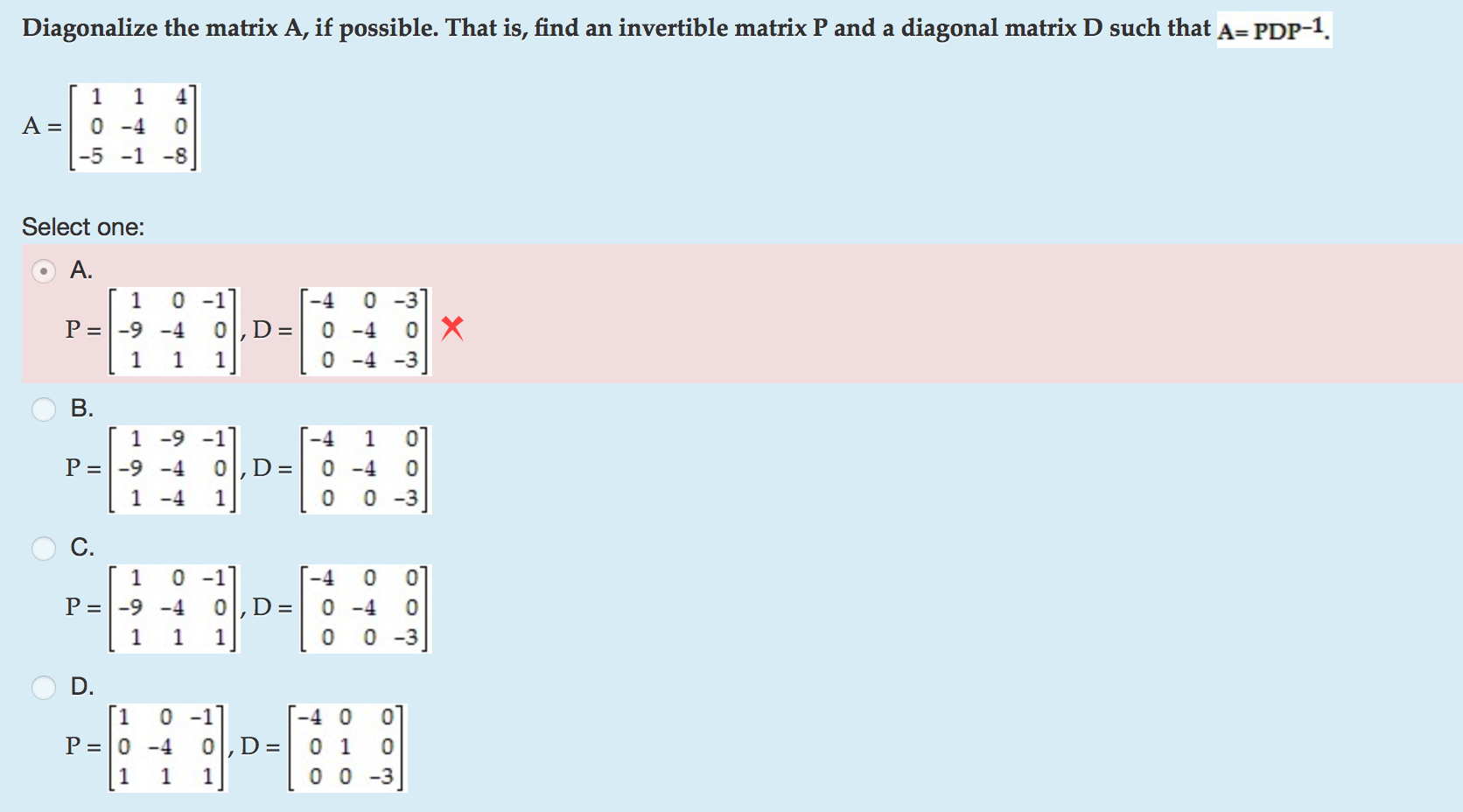
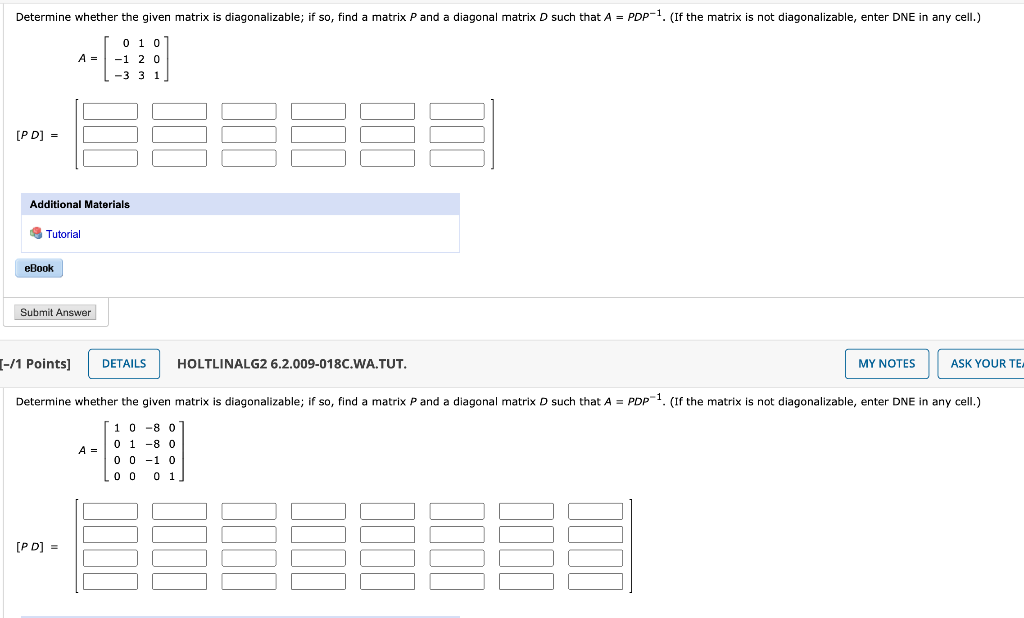
Find the eigen values using the equation given below. Notice that a matrix is diagonalizable if and only if it is similar to a diagonal matrix. A matrix with characteristic polynomial λ 3 − 3 λ 2 + 2 λ must be diagonalizable.

First i found the lambda's that make this zero (eigenvalues). When a matrix is similar to a diagonal matrix, the matrix is said to be diagonalizable. Matrix, the one with numbers,.

Skip to the 4 ways:. 119k views 4 years ago linear algebra. Find the eigenvalues of your given matrix.

Learn how to find a basis of eigenvectors of a matrix a and show that a is diagonalizable if and only if a has an eigenbasis. We have, however, seen several examples of a matrix \(a\) that is not. Apply the diagonalization equation using the.

Using the diagonalize matrix calculator. Testing if a matrix is diagonalizable. There are three ways to know whether a matrix is diagonalizable:

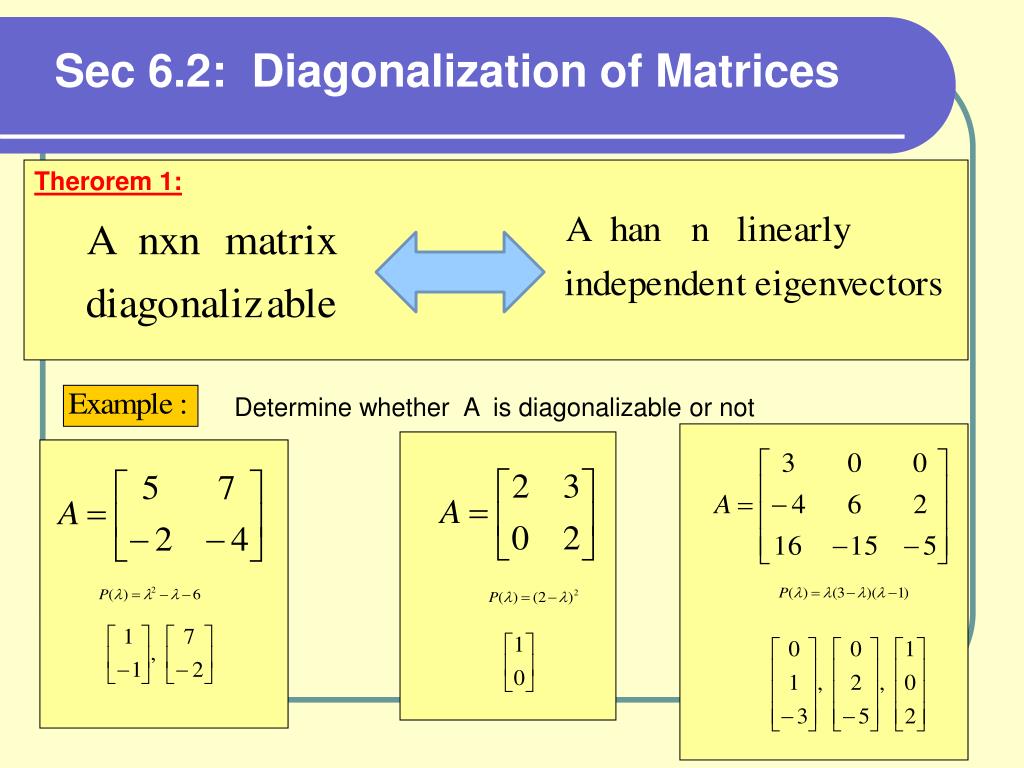
A square matrix of order n is diagonalizable if it has n linearly independent eigenvectors, in other words, if. Learn the criterion for diagonalizability, the eigenvalue problem, and how to take powers of a diagonalizable. A is diagonalizable if and only if for every eigenvalue λ of a, the algebraic multiplicity of λ is equal to the geometric multiplicity of λ.

That is, if there exists an invertible \(n\times n\) matrix \(c\) and a diagonal. I.e., given a real symmetric matrix , is diagonal for some orthogonal matrix. Welcome to the diagonalize matrix calculator, where we'll take you on a.

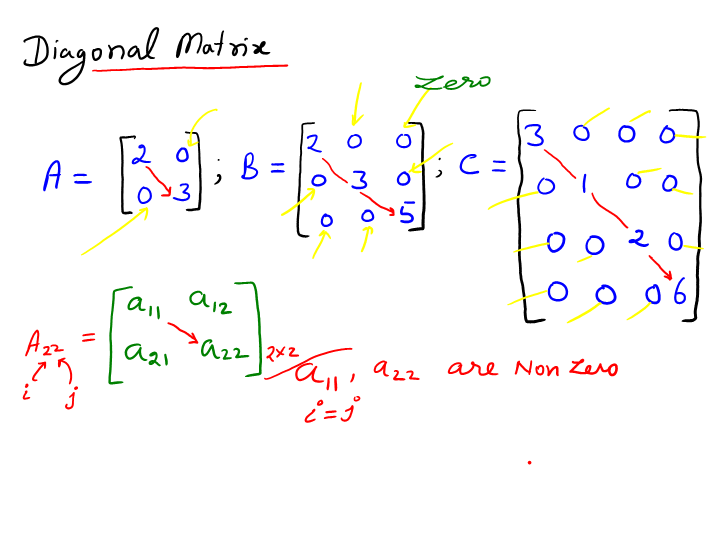
Use the eigenvalues to get the eigenvectors. Initialize the diagonal matrix d as: An \(n\times n\) matrix \(a\) is diagonalizable if it is similar to a diagonal matrix:

If \ (a\) is an \ (n\times n\) matrix with \ (n\) distinct. We define a diagonal matrix \(d\) as a matrix containing a zero in. Things you should know.